EMA 對比 SMA:哪種移動平均線更好?
移動平均線是交易中常用的技術指標,用於識別趨勢和潛在支點。在本文中,我們將探討兩種常用的移動平均值:簡單移動平均值 (SMA) 和指數移動平均值 (EMA)。我們將討論何時使用它們,以及它們的優缺點,以便您更好地瞭解策略中使用的移動平均值。
主要收穫:
移動平均線有助於平滑價格數據,識別趨勢和潛在支點。
簡單移動平均線 (SMA) 爲每個數據點提供同等權重,適合長期趨勢識別。
指數移動平均線 (EMA) 對近期數據更爲重視,因此對當前市場行情的反應更爲迅速。
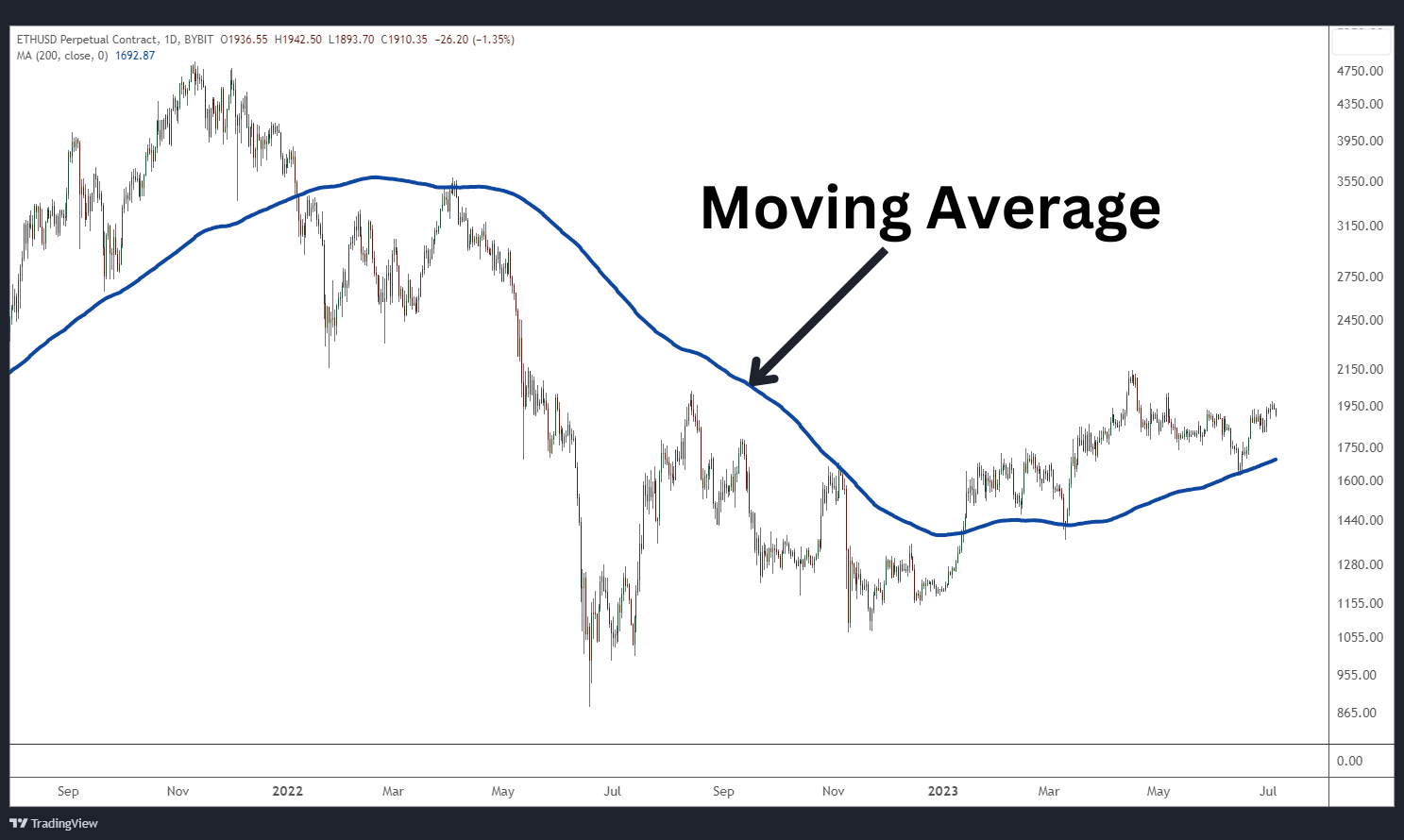
什麼是移動平均線?
移動平均線是技術分析中最常用的工具之一。爲了透過計算特定時間段內的平均價格來消除價格波動,交易者可以識別趨勢和潛在的支點。
移動平均值顯示爲圖表價格操作的一條線。這是一個多功能的技術指標,可用於任何圖表時間範圍,從短期日內圖表到長期每週或每月圖表。交易者依賴移動平均線提供的寶貴見解,例如確定整體趨勢方向和過濾市場噪音,做出更明智的交易決策。
移動平均線有多種類型,但此處的重點是 SMA 和 EMA。
什麼是簡單移動平均線 (SMA)?
最常用的移動平均線類型之一是簡單的移動平均線 (SMA)。其計算簡單明瞭,能夠可靠地反映之前的價格數據。大型機構使用 SMA 分析長期價格趨勢。
何時使用簡單移動平均線
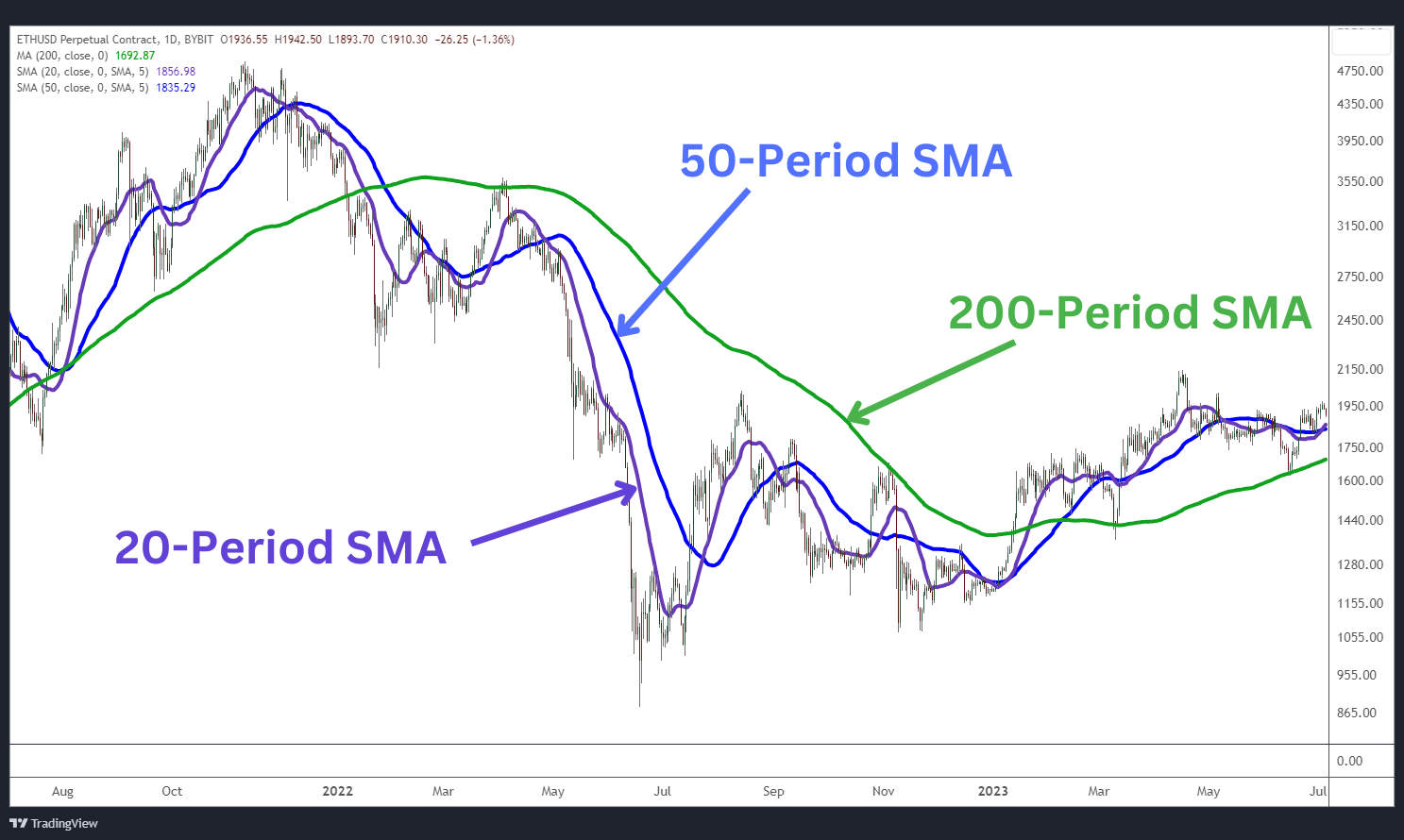
許多交易者在識別長期趨勢時使用 SMA。因此,它通常用於每日、每週或每月的時間範圍,輸入值爲 10、20、50 或 200。
簡單的移動平均值與價格序列中的每個數據點的權重相等。這意味着近期價格在計算中的權重與舊數據點相同。因此,SMA 對價格大幅波動的反應速度較慢。
交易者通常會將 SMA 與其他技術分析工具結合使用,來確認或驗證信號。例如,如果交易策略包含多個時間範圍分析,則大多數交易者將在較大的圖表時間範圍內使用 200 期 SMA 作爲識別趨勢的長期平均值。
當資產價格始終高於 SMA 時,表明存在上漲趨勢,表明存在潛在買入機會。相反,當價格持續低於 SMA 時,則表明價格呈下跌趨勢,表明可能存在賣出機會。
日間交易者可以將較小的輸入值納入其 SMA,例如 10 期或 20 期。這有助於加快移動平均線的速度,使其對價格波動更加敏感,從而快速應對任何短期交易。
最後,不同 SMA 期間之間的交叉是一種流行策略,在網絡上共享,用於生成交易信號。但是,SMA 跨界交易策略往往遲於新趨勢,因此,如果您正在考慮,請格外小心。
如何計算簡單移動平均值
SMA 的計算方式爲:將特定時間段內資產的收盤價相加,然後將總和除以週期數。計算 SMA 是一個簡單的數學公式,幸運的是,您無需記住它,因爲當日製圖包將自動爲您執行計算。
例如,要計算 10 天的 SMA,您需要將資產過去 10 天的收盤價相加,並將總和除以 10。每天,最早的收盤價都會下跌,最新的收盤價也會添加到計算中,從而創造出能夠持續適應近期價格的移動平均值。
計算簡單移動平均值的步驟如下:
確定移動平均線(例如 10、50 或 200)的週期數。
在最新價格數據上將指定時間段內的資產收盤價格相加。
將總和除以週期數。
現在,我們來計算 10 天 SMA,收盤價如下:$25、$27、$26、$28、$29、$31、$30、$29、$28 和 $27。
收盤價總和 = $25 + $27 + $26 + $28 + $29 + $31 + $30 + $29 + $28 + $27 = $280
10 天 SMA = $280 / 10 = $28
在每個交易日重複此流程,即可在圖表上繪製 SMA,以直觀顯示指定時間段內的平均價格波動。
請記住,SMA 期間的選擇取決於您的策略和所分析的時間範圍。較短的週期對價格變化的反應更快,而較長的週期則提供更平穩的平均值,反映出更重大的趨勢。
什麼是指數移動平均線 (EMA)?
除了簡單的移動平均值外,另一個熱門的技術分析指標是指數移動平均值。儘管與 SMA 類似,EMA 對近期數據更爲重視,因此對當前市場行情的反應也更爲迅速。
EMA 計算與 SMA 的不同之處在於,它包含平滑因子,可指數地降低舊價格數據的權重。這意味着 EMA 更重視當前價格,能夠快速應對市場趨勢的變化。
何時使用指數移動平均值
EMA 對更傾向於關注短期趨勢和價格走勢的交易者特別有用。由於 EMA 注重近期價格,因此與 SMA 相比,EMA 更適合捕捉和應對快速價格變化。以下是 EMA 可能有益的一些場景。
識別趨勢變化:EMA 可幫助交易者比簡單的移動平均線更早發現潛在趨勢逆轉。由於 EMA 對價格走勢的反應更快,因此當趨勢即將改變方向時,EMA 可提供及時信號。
騎行動力:希望利用短期價格波動和勢頭的交易者通常依賴 EMA。使用更短的 EMA 週期,他們可以根據即時價格走勢快速進入和退出交易。
交易突破:突破交易者會尋找突破關鍵支撐或阻力水平的價格走勢。由於 EMA 響應速度更快,因此價格突破錶明價格呈看漲趨勢,而低於 EMA 的價格突破則表明價格可能出現看跌趨勢。
如何計算指數移動平均值
與 SMA 相比,EMA 的計算公式略複雜。公式包含一個乘數,用於決定每個價格數據點的權重。以下是計算 EMA 的步驟:
確定您希望用於 EMA 的期間數。
使用以下公式計算平滑係數 (SF):SF = 2 / (N + 1),其中 N 表示週期數。
以第一期的 SMA 作爲初始 EMA 值。
對於每個後續週期,使用以下公式計算 EMA:EMA = (當前價格 − 先前 EMA) × SF + 先前 EMA
對每個週期重複此計算,並相應更新 EMA 值。
使用上述公式,計算出收盤價爲 $25、$27、$26、$28、$29、$31、$30、$29、$28 和 $27 的股票的 10 天 EMA。
我們將計算 10 期 EMA。
確定平滑係數:SF = 2 / (10 + 1) = 0.1818
從 10 天 SMA 開始,作爲初始 EMA 值:EMA = $28
計算第二階段的 10 天 EMA:EMA = ($27 − $28) × 0.1818 + $28 = $27.1818
對後續每個週期重複此計算,獲得 EMA 值。
透過在圖表上繪製 EMA,交易者可以直觀地分析價格與 EMA 線之間的關係,從而發現潛在的交易機會並做出明智的決策。
請記住,EMA 期間的選擇取決於策略和對價格變化的預期響應程度。EMA 週期更短,反應速度更快,但可能更容易受到虛假信號的影響,而 EMA 週期更長,可提供更平穩的平均值,但對價格走勢的反應更慢。
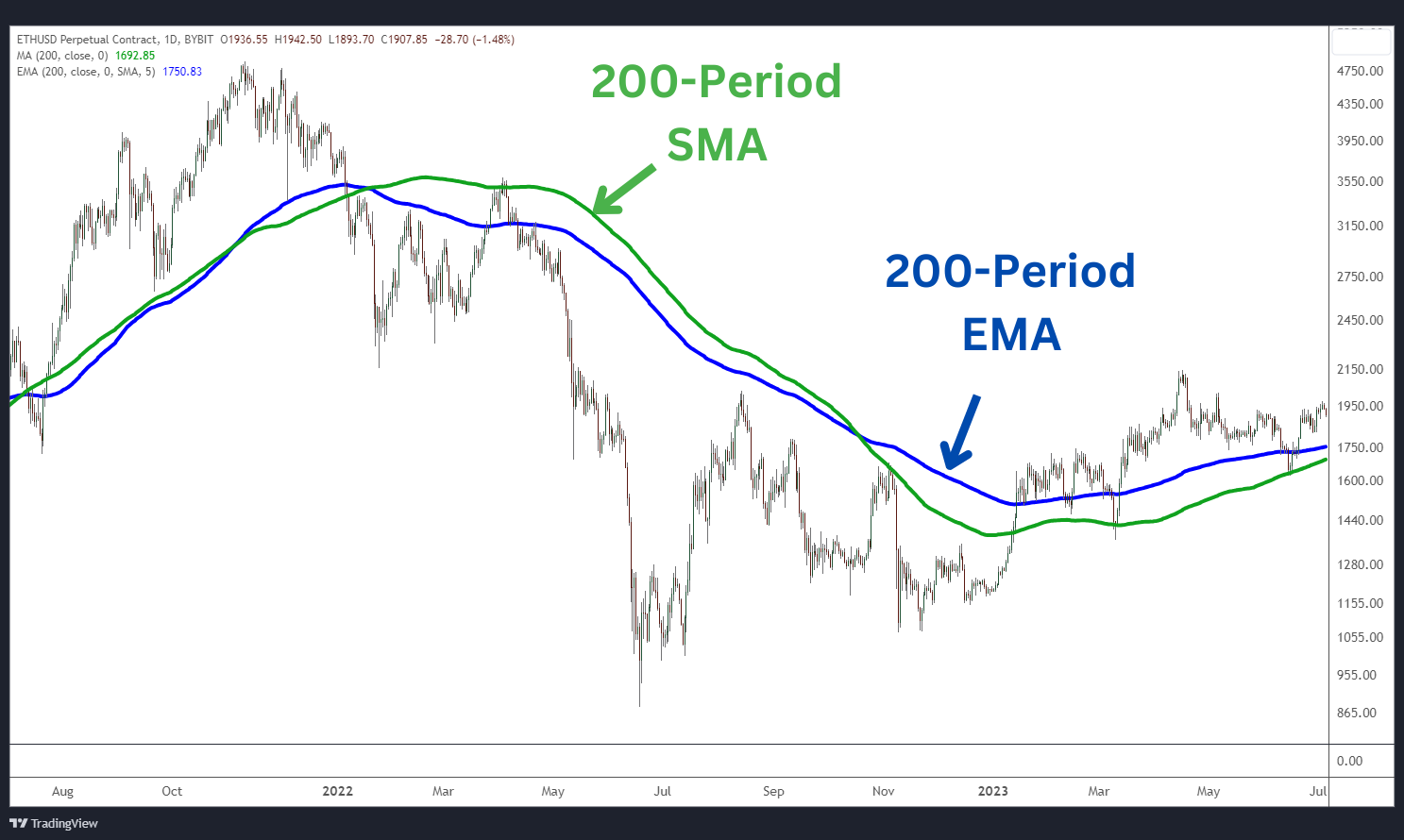
EMA 與 SMA 的主要區別
雖然指數移動平均線 (EMA) 和簡單移動平均線 (SMA) 通常用於技術分析,但它們存在一些關鍵差異。下面是一個對比表,重點介紹了它們的區別。
EMA | SMA | |
計算 | 指數加權 — 爲近期價格走勢賦予更多權重 | 權重均等 — 與所有價格數據權重均等 |
響應能力 | 對近期價格變化反應更迅速 | 對近期價格變化的反應較差 |
滯後 | 與 SMA 相比,滯後時間更短 | 與 EMA 相比滯後更多 |
線條流暢度 | 響應速度更快,可能會導致波動更不穩定 | 信號線更流暢、更穩定 |
EMA 優於 SMA 的優勢
與 SMA 相比,EMA 具有多種優勢,是衆多交易者的熱門選擇。
響應能力:EMA 對當前價格變化作出快速響應,使交易者能夠更迅速地捕捉趨勢和潛在交易機會。
及時信號:由於 EMA 注重當前價格,因此能夠及時提供市場趨勢逆轉和進場/出場點信號。
降低滯後:EMA 的滯後率低於 SMA,使交易者能夠根據當前市場行情更快地做出決策。
SMA 優於 EMA 的優勢
儘管 EMA 具有優勢,但 SMA 也具有以下獨特優勢:
簡單易用:SMA 的計算非常簡單,所有經驗水平的交易者都能理解。
流暢度:SMA 提供更順暢、更穩定的信號線,減少短期價格波動的影響,提供更清晰的整體趨勢圖。
可靠性: 從小型交易者到大型機構,SMA 得到更廣泛的關注。這使得圍繞信號的信號更加可靠。
哪一種移動平均線更適合日間交易?
儘管這兩種移動平均線均用於日間交易,交易者希望在單個交易日內利用短期價格波動,但指數移動平均線往往是首選。他們對近期價格變化的響應使日間交易者能夠快速識別和應對日內趨勢和價格反轉,從而提供更及時的入場和出場信號。
哪個移動平均線更適合散倉交易?
在波動交易方面,一種涉及在數天至數週內捕獲中期價格波動的策略,指數移動平均線和簡單移動平均線均可有效。EMA 和 SMA 之間的選擇取決於交易者的偏好。EMA 對當前價格的響應有助於波動交易者識別短期波動,並捕捉較小的價格波動。另一方面,許多波動交易者採用了某種多時間幀分析,使 SMA 的流暢性和穩定性更加可靠,並更清晰地瞭解整體趨勢。
結語
簡單的移動平均值和指數移動平均值是重要的技術指標。每個移動平均線都有其優勢,適用於不同的交易策略和時間範圍。SMA 提供更流暢、更穩定的信號線,使其能夠可靠地識別長期趨勢。另一方面,EMA 對近期價格變化的響應能力非常適合短期趨勢識別和縮短價格波動。透過瞭解這兩種移動平均線的區別和優勢,交易者可以增強分析能力,做出更明智的交易決策。
#Bybit #TheCryptoArk